Introduction
This post is going to explain the basic idea behind a Minkowski difference – what they are, how to visualize them geometrically, and a simple case of leveraging them for collision detection. The intent is to give you a solid intuition for a concept that is very fundamental in many collision detection algorithms, as well as what problems you need to solve to extend my basic presentation of it!
This guide uses the case where your game geometry is 2D, axis aligned rectangles, which can cover pretty much any 2D game that only needs basic collision detection. The methods in this article can be extended to more general cases, too.
Minkowski Difference
what is a minkowski difference?
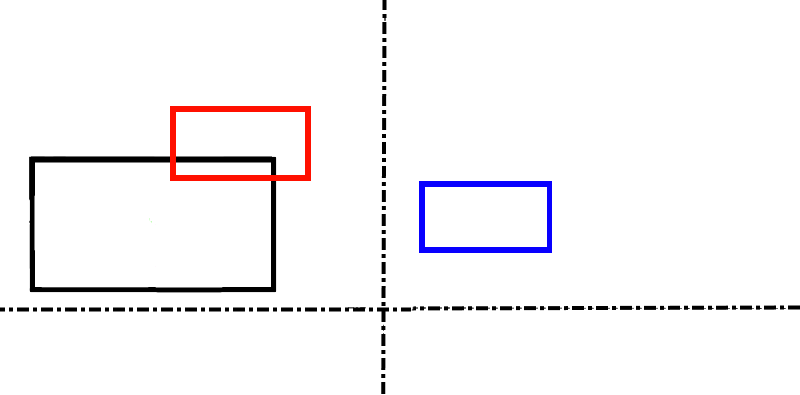
Geometrically, the Minkowski difference of two 2D shapes is the shape produced when you subtract every point on one shape from every point on the other shape. Here’s an example. We’re going to find the Minkowski difference of the blue rectangle and the red rectangle. Let’s do this by corners. We will subtract one corner at a time. Start with subtracting the bottom left corner of the blue from every point on the red. The black vector is the vector we’re subtracting. The green rectangle is the resulting shape.
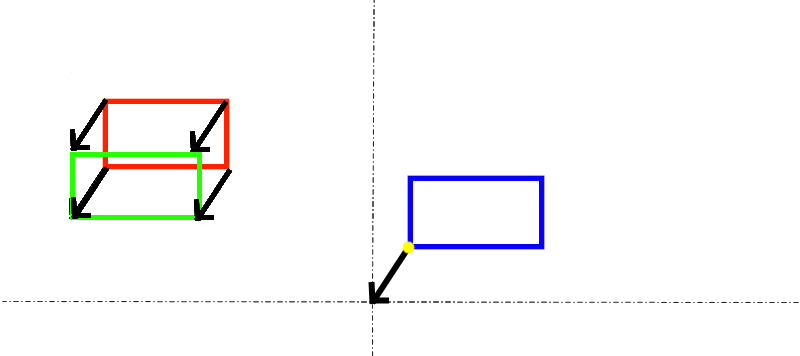
That wasn’t so bad! But aren’t there infinitely many points on a rectangle? How are we going to subtract ALL of them, given that my computer only runs at about 3 GHz? The answer is that we don’t need to do all of the infinitely many points to see where this is going, thankfully. For our case of axis-aligned rectangles, simply subtracting the corners and filling in the gaps will give us exactly what we need. Let’s do another corner.
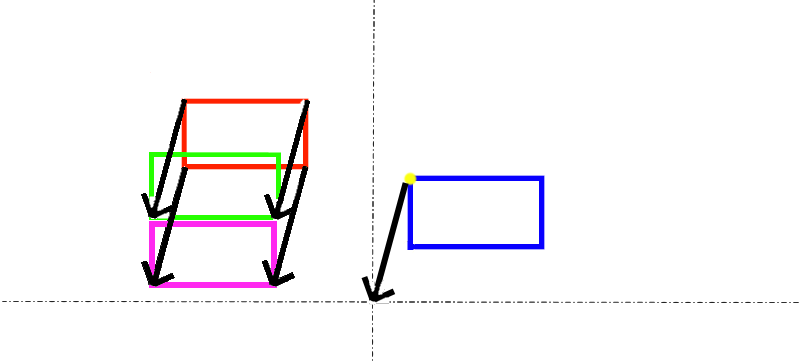
The purple rectangle is the same as the green rectangle, but shifted down by the height of the blue rectangle. From these two corners, we can see that every point between the top of the green rectangle and the bottom of the purple rectangle is included in the Minkowski difference. Hence, doing this little process on the corners gives us the extremes of the Minkowski difference. To visualize the rest of the shape, we can just fill in the middle! If you do this process for all four corners, you end up with this:
There we go! That’s the Minkowski difference of these two rectangles! The top right of this black rectangle is exactly the green rectangle from step one. Ditto for the bottom right corner and the purple rectangle from step two. You can see that something which sounds confusing like ‘subtract every point on one shape from every point on another shape’ really has a straightforward geometric interpretation in this context.
are we still talking about collisions?
Now, the question becomes: How can we leverage this to do collision detection? The answer is pretty simple. What does it mean for two boxes to collide? Well, one way of formulating the answer to that is that there exists some point which lies inside both boxes. The beauty of the Minkowski method is that it encodes this condition perfectly. If two boxes contain the same point, then when we subtract those two points, we’ll get the origin. Therefore, if the Minkowski difference of box A and box B contains the origin, the two boxes must be share a point, and are colliding!
Now our algorithm for doing collision detection should be super clear! All we have to do is:
- Find the Minkowski difference (which is just a rectangle) of the two bounding boxes
- Check if the origin lies inside the Minkowski box
finding the minkowski difference algorithmically
This is an extremely simple calculation once you understand the intuition behind it. What we’re going to do is figure out the coordinates of the four corners of the Minkowski difference. The first thing to notice is that subtracting the bottom points on the blue rectangle from the top points on the red rectangle makes the top of the Minkoswki difference. This makes sense: To maximize A - B, you want the biggest A and the smallest B from your pool of numbers. Our pool of numbers for A is all the Y values on the red rectangle. Our pool of numbers for B is all the Y values on the blue rectangle. Maximizing A means choosing the top of the red rectangle. Minimizing B means choosing the bottom of the blue rectangle, and so we get the largest difference we possibly could.
Similarly, subtracting the leftmost points of the blue rectangle from rightmost points of the red rectangle gives us the rightmost points of the Minkowski difference. Combining these two ideas, subtracting the bottom left of the blue rectangle from the top right of the red rectangle gives us the top right of the Minkowski difference. If you follow this strategy to its conclusion, you get these equations:
black.top_right = red.top_right - blue.bottom_left;
black.top_left = red.top_left - blue.bottom_right;
black.bottom_right = red.bottom_right - blue.top_left;
black.bottom_left = red.bottom_left - blue.top_right;
// Or, if you prefer:
black.top = red.top - blue.bottom;
black.bottom = red.bottom - blue.top;
black.left = red.left - blue.right;
black.right = red.right - blue.left;
This isn’t the only way to calculate the Minkowski difference, but I think it’s the easiest, and it’s fast enough that you don’t really need another method. If your rectangles are stored in origin + extents format, you can easily convert them to four-corners and then do this calculation – slightly inefficient, but on modern hardware not even a second thought. Drop me a message on Twitter if you really need to know how to use origin + extents without converting!
The last thing we have to know is whether this box encompasses the origin. This is extremely simple! We just need to check that left <= 0 <= right, and bottom <= 0 <= top.
if (verts.right >= 0 && verts.left <= 0 && verts.top >= 0 && verts.bottom <= 0) {
// handle that bad boy
}
Collision Resolution
what is collision resolution?
So you’ve determined there is a collision between two objects. This is pretty useless information on its own unless you know how to fix the objects’ locations so that they are not colliding! Collision resolution is exactly this – once you figure out how two objects are colliding, you also figure out how to scoot them in the right direction so that they aren’t colliding when the frame ends.
There can be two kinds of objects in any game: static and moving. Static things don’t move, like a building. Moving things do, like a player or a bullet. Since two static things can’t collide, for collisions you only have to worry about two cases: static + moving (e.g. the player walking into a building) and moving + moving (e..g player colliding with an enemy).
penetration vector
A penetration vector is a vector that tells us exactly how far and in what direction two objects are colliding. More specifically, it is the smallest vector that when applied to one of two colliding objects will make them not collide. If we know this vector, we know how to handle a collision – we know how far to move the object back, and we know in what direction to move it. Luckily, it’s super easy to get the penetration vector from the Minkowski difference.
Here’s the intuition: We want to find the shortest vector that makes our boxes not collide. This is the same as saying we want to find the shortest vector that will make the Minkowski difference not contain the origin.
We know that this vector must be straight up, down, left, or right – if you could move the box diagonally to get it off the origin (think of this as the hypotenuse of a triangle), then one of the legs of the triangle must also get it off the origin. Since legs are shorter than hypotenuse, using the axis-aligned leg must be shorter, and so is a better penetration vector.
Knowing this, the smallest straight vector that gets the Minkowski box off of the origin is the smallest value of the left, right, top or bottom that defines the box. Here’s the algorithm:
- Choose the smallest value of the top, bottom, left, and right
- If the smallest value is the top or bottom, the penetration vector is (0, top or bottom)
- If the smallest value is the left or right, the penetration vector is (left or right, 0)
bool are_boxes_colliding(Box a, Box b, vec2& penetration) {
// First, calculate the Minkowski difference. a maps to red, and b maps to blue from our example (though it doesn't matter!)
Box minkowski;
minkowski.top = a.top - b.bottom;
minkowski.bottom = a.bottom - b.top;
minkowski.left = a.left - b.right;
minkowski.right = a.right - b.left;
minkowski.extents = a.extents + b.extents;
// If the Minkowski difference intersects the origin, there's a collision
if (verts.right >= 0 && verts.left <= 0 && verts.top >= 0 && verts.bottom <= 0) {
// The pen vector is the shortest vector from the origin of the MD to an edge.
// You know this has to be a vertical or horizontal line from the origin (these are by def. the shortest)
float min = FLOAT_MAX_VALUE;
if (abs(verts.left) < min) {
min = abs(verts.left);
penetration = glm::vec2(verts.left, 0.f);
}
if (abs(verts.right) < min) {
min = abs(verts.right);
penetration = glm::vec2(verts.right, 0.f);
}
if (abs(verts.top) < min) {
min = abs(verts.top);
penetration = glm::vec2(0.f, verts.top);
}
if (abs(verts.bottom) < min) {
min = abs(verts.bottom);
penetration = glm::vec2(0.f, verts.bottom);
}
return true;
}
penetration = glm::vec2(0.f);
return false;
}
And there you have it. We’ve successfully written a function which can determine if two axis-aligned 2D boxes are colliding and, if so, give us a vector that will rectify that collision. If your collision is moving vs static, just have the entity that is moving move back by this vector. This is akin to having the player stop when they run and collide into a wall. If your collision is two moving entities, it is a bit more complicated – you probably want both the entities to move a little bit rather than just one butting the other out.
In many 2D games, though, you can just fake it. If your game is based around its physics system, you will probably want the real thing. However, for an RPG (for example), there aren’t enough moving parts in your game to warrant the effort. There are a lot of edge cases when resolving collisions between two things that move!
One simple one (but still headache inducing): Mario jumps on a Goomba. You try to move the Goomba downward along the penetration vector. Now the Goomba is in the floor, so your collision system moves it upward along the penetration system. Your computer experiences a sense of deep philosophical confusion as it spents all of eternity rearranging one Goomba. The purpose of this article is understanding Minkowski differences and how they can be interpreted geometrically in 2D, so I am going to skip the more difficult aspects of collision resolution.
If you have any questions or would like me to expand on anything I have written here (or would just like to say hello), shoot me an email at thomas (dot) spader (at) gmail (dot) com.
Related Links
Collision detection in games is really derived from math. Specifically, the math of what are called convex sets. Here is an excellent lecture videwo introducing you to convex sets. This may be a bit heavy without a moderate background in math – but you can do it if you got this far!
Casey Muratori’s excellent video explaining GJK, a popular algorithm for doing collision detection in 3D.